Cache Design
LRU State Machine
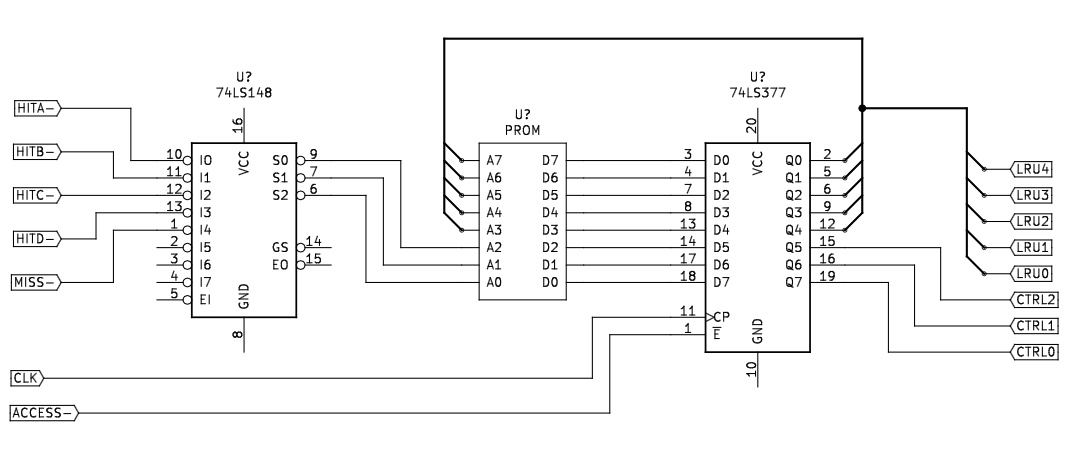
The following tables define the states and transitions of a ROM-based state machine to implement the Least Recently Used (LRU) logic for a 4-way set associative cache. The current and next state indicate the reverse order of when the four sets A through D were accessed, so "ABCD" means A is most recently used and D is least recently used. The next state is chosen based on the current state and whether there was a hit on set A through D or a miss.
This state machine has 24 possible states and 120 transitions. It should fit in a 256 x 8 ROM and register, with the current LRU state as bits 0-4 of the address, the matching set as bits 5-6, and miss signal as bit 7. Bits 0-4 of the output register would be written back to the LRU state. The remaining bits of the output can be used to indicate whether the LRU data for an entry should be updated and which set should be replaced.
Key
| Code | Definition |
|---|---|
| A | Set A |
| B | Set B |
| C | Set C |
| D | Set D |
| M | Miss |
| N | No Operation |
| R | Replace |
| U | Update |
State Transition Table
| Current | Index | Input | Next | Action |
|---|---|---|---|---|
| CDAB | 16:0 | A | ACDB | U |
| CDAB | 16:1 | B | BCDA | U |
| CDAB | 16:2 | C | CDAB | N |
| CDAB | 16:3 | D | DCAB | U |
| CDAB | 16:4 | MISS | BCDA | R |
| CDBA | 17:0 | A | ACDB | U |
| CDBA | 17:1 | B | BCDA | U |
| CDBA | 17:2 | C | CDBA | N |
| CDBA | 17:3 | D | DCBA | U |
| CDBA | 17:4 | MISS | ACDB | R |
| DABC | 18:0 | A | ADBC | U |
| DABC | 18:1 | B | BDAC | U |
| DABC | 18:2 | C | CDAB | U |
| DABC | 18:3 | D | DABC | N |
| DABC | 18:4 | MISS | CDAB | R |
| DACB | 19:0 | A | ADCB | U |
| DACB | 19:1 | B | BDAC | U |
| DACB | 19:2 | C | CDAB | U |
| DACB | 19:3 | D | DACB | N |
| DACB | 19:4 | MISS | BDAC | R |
| DBAC | 20:0 | A | ADBC | U |
| DBAC | 20:1 | B | BDAC | U |
| DBAC | 20:2 | C | CDBA | U |
| DBAC | 20:3 | D | DBAC | N |
| DBAC | 20:4 | MISS | CDBA | R |
| DBCA | 21:0 | A | ADBC | U |
| DBCA | 21:1 | B | BDCA | U |
| DBCA | 21:2 | C | CDBA | U |
| DBCA | 21:3 | D | DBCA | N |
| DBCA | 21:4 | MISS | ADBC | R |
| DCAB | 22:0 | A | ADCB | U |
| DCAB | 22:1 | B | BDCA | U |
| DCAB | 22:2 | C | CDAB | U |
| DCAB | 22:3 | D | DCAB | N |
| DCAB | 22:4 | MISS | BDCA | R |
| DCBA | 23:0 | A | ADCB | U |
| DCBA | 23:1 | B | BDCA | U |
| DCBA | 23:2 | C | CDBA | U |
| DCBA | 23:3 | D | DCBA | N |
| DCBA | 23:4 | MISS | ADCB | R |
| Current | Index | Input | Next | Action |
|---|---|---|---|---|
| BCAD | 8:0 | A | ABCD | U |
| BCAD | 8:1 | B | BCAD | N |
| BCAD | 8:2 | C | CBAD | U |
| BCAD | 8:3 | D | DBCA | U |
| BCAD | 8:4 | MISS | DBCA | R |
| BCDA | 9:0 | A | ABCD | U |
| BCDA | 9:1 | B | BCDA | N |
| BCDA | 9:2 | C | CBDA | U |
| BCDA | 9:3 | D | DBCA | U |
| BCDA | 9:4 | MISS | ABCD | R |
| BDAC | 10:0 | A | ABDC | U |
| BDAC | 10:1 | B | BDAC | N |
| BDAC | 10:2 | C | CBDA | U |
| BDAC | 10:3 | D | DBAC | U |
| BDAC | 10:4 | MISS | CBDA | R |
| BDCA | 11:0 | A | ABDC | U |
| BDCA | 11:1 | B | BDCA | N |
| BDCA | 11:2 | C | CBDA | U |
| BDCA | 11:3 | D | DBCA | U |
| BDCA | 11:4 | MISS | ABDC | R |
| CABD | 12:0 | A | ACBD | U |
| CABD | 12:1 | B | BCAD | U |
| CABD | 12:2 | C | CABD | N |
| CABD | 12:3 | D | DCAB | U |
| CABD | 12:4 | MISS | DCAB | R |
| CADB | 13:0 | A | ACDB | U |
| CADB | 13:1 | B | BCAD | U |
| CADB | 13:2 | C | CADB | N |
| CADB | 13:3 | D | DCAB | U |
| CADB | 13:4 | MISS | BCAD | R |
| CBAD | 14:0 | A | ACBD | U |
| CBAD | 14:1 | B | BCAD | U |
| CBAD | 14:2 | C | CBAD | N |
| CBAD | 14:3 | D | DCBA | U |
| CBAD | 14:4 | MISS | DCBA | R |
| CBDA | 15:0 | A | ACBD | U |
| CBDA | 15:1 | B | BCDA | U |
| CBDA | 15:2 | C | CBDA | N |
| CBDA | 15:3 | D | DCBA | U |
| CBDA | 15:4 | MISS | ACBD | R |
| Current | Index | Input | Next | Action |
|---|---|---|---|---|
| ABCD | 0:0 | A | ABCD | N |
| ABCD | 0:1 | B | BACD | U |
| ABCD | 0:2 | C | CABD | U |
| ABCD | 0:3 | D | DABC | U |
| ABCD | 0:4 | MISS | DABC | R |
| ABDC | 1:0 | A | ABDC | N |
| ABDC | 1:1 | B | BADC | U |
| ABDC | 1:2 | C | CABD | U |
| ABDC | 1:3 | D | DABC | U |
| ABDC | 1:4 | MISS | CABD | R |
| ACBD | 2:0 | A | ACBD | N |
| ACBD | 2:1 | B | BACD | U |
| ACBD | 2:2 | C | CABD | U |
| ACBD | 2:3 | D | DACB | U |
| ACBD | 2:4 | MISS | DACB | R |
| ACDB | 3:0 | A | ACDB | N |
| ACDB | 3:1 | B | BACD | U |
| ACDB | 3:2 | C | CADB | U |
| ACDB | 3:3 | D | DACB | U |
| ACDB | 3:4 | MISS | BACD | R |
| ADBC | 4:0 | A | ADBC | N |
| ADBC | 4:1 | B | BADC | U |
| ADBC | 4:2 | C | CADB | U |
| ADBC | 4:3 | D | DABC | U |
| ADBC | 4:4 | MISS | CADB | R |
| ADCB | 5:0 | A | ADCB | N |
| ADCB | 5:1 | B | BADC | U |
| ADCB | 5:2 | C | CADB | U |
| ADCB | 5:3 | D | DACB | U |
| ADCB | 5:4 | MISS | BADC | R |
| BACD | 6:0 | A | ABCD | U |
| BACD | 6:1 | B | BACD | N |
| BACD | 6:2 | C | CBAD | U |
| BACD | 6:3 | D | DBAC | U |
| BACD | 6:4 | MISS | DBAC | R |
| BADC | 7:0 | A | ABDC | U |
| BADC | 7:1 | B | BADC | N |
| BADC | 7:2 | C | CBAD | U |
| BADC | 7:3 | D | DBAC | U |
| BADC | 7:4 | MISS | CBAD | R |
State Table Generator
State is a Java program that generates all the possible LRU states for an N-way set associate cache, then generates a state transition table. The purpose of this program was to determine the most efficient way to implement the logic in a lookup table.
For example, the most straight-forward approach would be to have 8 bits to encode the LRU state, 2 bits to encode the match, and a bit to indicate a miss. This would require a 2048 x 10 ROM (assuming 2 additional bits to encode the action). This is inefficient because there are only 24 possible states. This can be encoded in 5 bits, so we only need a 256 x 7 ROM.
This inefficiency grows exponentially as the number of sets increases. A simple lookup table for an 8-way cache would require 24 bits (8 x 3) to encode the state plus 4 additional bits to encode the matching set or miss. That would be untenable. The cache actually has only 40320 possible states which can be encoded in 16 bits. That's still a large ROM, but much more tenable than having a 28 bit address!